2. Metoda symulacji - przykład
2.1. Opis sytuacji
2.2. Model symulacyjny
2.3. Wykonanie symulacji
2.4. Analiza wyników
3. Metoda Monte Carlo - przykład
3.1. Metoda Monte Carlo
3.2. Zastosowanie metody MC
3.3. Modelowanie niepewności
3.4. Model symulacyjny
3.5. Wykonanie symulacji
3.6. Analiza wyników
4. Statystyczne aspekty symulacji
4.1. Wprowadzenie
4.2. Liczby losowe
4.3. Liczby pseudolosowe
4.4. Pobieranie próbek z rozkładów
4.5. Analiza wyników
4.6. Metody redukcji wariancji
5.1. Model jednokanałowej kolejki
5.2. Stochastyczny model systemu zapasów
Druga połowa lat 70. - prognoza, że przewozy główną linią CNR (Canadian National Railway) podwoją się w następnej dekadzie. Przewidywano konieczność wydania 2,2 mld CAD, z tego 1,3 mld na zbudowanie drugiego toru. Kosztem 300 tys. zbudowano model symulacyjny i przeprowadzono nań eksperymenty. Okazało się, że nie wszędzie potrzebne są 2 tory: nie wybudowano odcinka o długości 128 mil. Efekt: oszczędność około 300 mln
CAD.Jest to metoda polegająca na badaniu zachowania się systemu przy użyciu modeli realizowanych na maszynach cyfrowych. Pod pojęciem systemu rozumieć będziemy pewien zbiór powiązanych ze sobą obiektów scharakteryzowanych przy pomocy atrybutów (cech), które również mogą być ze sobą powiązane. Zakładamy, że ich struktura nie podlega zmianom, a jedynie cechy poszczególnych obiektów mogą przyjmować różne wartości w kolejnych chwilach czasu tzn. system osiąga kolejne stany pod wpływem zachodzących zdarzeń.
Innymi słowy symulacja jest metodą prowadzenia eksperymentu, w którym decydent buduje model imitujący (naśladujący) działanie rzeczywistego systemu. Poprzez eksperymenty z modelem, decydent może studiować charakterystykę i zachowanie się tegoż systemu w czasie. Jeżeli używamy modeli matematycznych mówimy o symulacji numerycznej. Czasem terminem tym określa się pewne typy iteracyjnych procedur obliczeniowych, w których często pobierane są próbki z rozkładów lecz czynnik czasu nie odgrywa
zasadniczej roli. Jest to tzw. metoda Monte Carlo.Rodzaje modeli symulacyjnych:
Ile kas ma być czynnych w banku?
Identyfikacja głównych części systemu: stanowiska obsługi i klienci.
Zdefiniowanie każdej operacji:
do systemu przybywa klient - w jaki sposób, np. wg rozkładu Poissona o określonej średniej lub zgodnie z danymi empirycznymi.
klient wybiera kolejkę - w jaki sposób: z reguły najkrótszą a jeśli są jednakowo długie - wg innych kryteriów.
przesuwanie się kolejki - reguła FIFO, czas obsługi losowany z rozkładu empirycznego lub np. normalnego z daną średnią i odchyleniem.
klient opuszcza system.
Symulację tego systemu zaczynamy od wylosowania momentu przybycia pierwszego klienta. Posyłamy go do wybranej wg jakiejś reguły kasy, gdzie jest natychmiast obsłużony. Wyznaczamy czas jego obsługi losując z odpowiedniego rozkładu i notujemy moment zakończenia. Następnie losujemy czas przybycia następnego klienta itd. Na każdym etapie musimy uważać, by we właściwej chwili wprowadzić każdego klienta, usunąć go z systemu, uaktualnić kolejkę po zakończeniu każdej obsługi.
W miarę trwania symulacji obliczamy też statystyki np. średni czas oczekiwania, średnia długość kolejki, łączny czas bezczynności kasjerek.
Ta prosta sytuacja ilustruje najważniejsze cechy symulacji:
Jest dobrze dostosowana do problemów, które są trudne lub wręcz niemożliwe do analitycznego rozwiązania.
Możliwość analizy “what if”. Modele optymalizacyjne odpowiadają na pytanie, jakie wartości zmiennych decyzyjnych są najlepsze dla przyjętej funkcji celu. Przyczyną powstania trudności jest zwykle złożoność rozpatrywanego modelu. Zastosowanie zwykłych metod analitycznych wymaga przyjęcia nierealistycznych założeń i uproszczeń. W tej sytuacji decydent może woleć określić zbiór decyzji, symulować rezultaty i obserwować, co się dzieje z kryterium.
Łatwa w użyciu. Symulacja nie wymaga skomplikowanego aparatu matematycznego. Decydent, który zna strukturę systemu może bez trudu opracować jego model przy użyciu aplikacji menadżerskich (np. arkusz kalkulacyjny). Model opisuje problem z punktu widzenia decydenta, który w łatwy sposób może go zrozumieć i kontrolować.
Kontrolowany eksperyment. Model symulacyjny explicite pokazuje najważniejsze relacje w rozważanym problemie. Dlatego decydenci używają modeli do systematycznego szacowania proponowanych polityk w symulowanych warunkach i do oceny wpływu kluczowych elementów na system. Eksperymenty te prowadzone są bez naruszania działania aktualnego systemu. Można w ten sposób uniknąć decyzji prowadzących do fatalnych następstw ekonomicznych, politycznych czy socjalnych.
Kompresja czasu. Eksperyment, który w rzeczywistym systemie trwałby miesiące czy lata, można przeprowadzić w ciągu kilku minut przy użyciu jego symulacyjnego modelu.
Laboratorium zarządzania. Model ilustruje i pozwala lepiej poznać rzeczywisty proces. Gry kierownicze pozwalają uczestnikom zrozumieć relacje między zmiennymi decyzyjnymi a rezultatami oraz rozwinąć umiejętności decyzyjne.
Nie gwarantuje optymalnego rozwiązania
. Podczas eksperymentu badane są tylko warianty podane przez użytkownika. Zawsze mogą istnieć lepsze układy zmiennych decyzyjnych, o których decydent nie ma pojęcia.Kosztowna. Modelowanie złożonego systemu, wykonywanie wielu obserwacji oraz pisanie programów jest bardzo pracochłonne nawet przy użyciu wyspecjalizowanych narzędzi. W celu oszacowania pojedynczej statystyki należy wielokrotnie powtarzać przebieg symulacji.
Pozorna łatwość stosowania. Często istnieje pokusa by stosować ją tam, gdzie można wyznaczyć rozwiązanie optymalne przy użyciu metod analitycznych. Ponadto nadmiar szczegółów wbudowanych w model może utrudnić przeprowadzenie eksperymentów.
Technika ta jest szeroko używana w biznesie i w instytucjach rządowych. Wg źródeł amerykańskich około 85% organizacji używa różnego rodzaju modeli symulacyjnych. Symulacja przybiera najróżniejsze formy od modelowania prostych systemów dla celów zarządzania operacyjnego (zapasy, produkcja, finanse, obsługa), poprzez gry menadżerskie, do modelowania wielkich systemów (korporacje, ekonomia światowa, pogoda). Symulacją jest również tzw. rzeczywistość wirtualna.

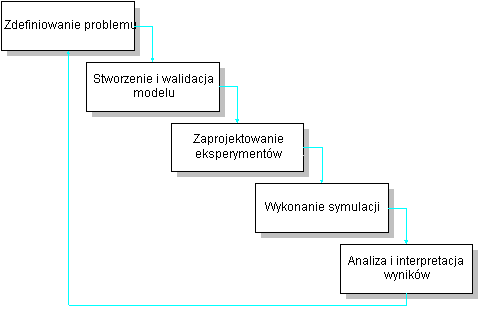
Zdefiniowanie problemu.
Zawiera przede wszystkim cele projektu i określenie przyczyn stosowania symulacji. Użytkownik powinien zdefiniować zarówno atrybuty interesujących cech jak i miary jakości rozwiązania. Ponadto należy określić zakres projektu i pożądany poziom szczegółowoś
ci.Stworzenie i walidacja modelu.
Ogólnie rzecz biorąc model identyfikuje kluczowe elementy problemu oraz ich relacje i ma przetransformować niekontrolowane i kontrolowane (decyzyjne) wejścia w zamierzone dane wyjściowe. Jeśli możemy dokładnie opisać zmienne niekontrolowane to mówimy o symulacji deterministycznej, jeśli zmienne te są opisane rozkładami statystycznymi - o symulacji probabilistycznej. Zmienne mogą mieć charakter dyskretny lub ciągły.
Estymacji parametrów modelu dokonuje się na podstawie bezpośrednich obserwacji lub danych historycznych. Parametry te i założenia modelu powinny być zweryfikowane przez doświadczonych użytkowników lub ekspertów. Po oprogramowaniu modelu, należy go zweryfikować statystycznie wprowadzając doń dane historyczne. W razie potrzeby należy model przebudować.
Zaprojektowanie eksperymentu.
W projekcie eksperymentu należy przede wszystkim określić warunki początkowe (np. czynna 1 kasa czy 2, w chwili t
0 przybywa do systemu 1,2,3 klientów). Jako że eksperyment ma dostarczyć odpowiedzi na pytania decydenta, należy ponadto przewidzieć wszystkie interesujące użytkownika wartości zmiennych decyzyjnych, dla których będą prowadzone oddzielne przebiegi.Wykonanie symulacji.
W przypadku symulacji deterministycznej prowadzimy tylko jeden przebieg dla każdej wartości zmiennej kontrolowanej.
W przypadku symulacji probabilistycznej wartości zmiennych niekontrolowanych są losowane z odpowiednich rozkładów, stąd każdy przebieg daje inne wyniki. By wyniki były statystycznie wiary-godne należy przeprowadzić kilkadziesiąt przebiegów dla każdej wartości zmiennej decyzyjnej.
Analiza rezultatów.
Analiza obejmuje porównanie symulowanych wyników otrzymanych z wyspecyfikowanych polityk. Ponieważ w przypadku symulacji probabilistycznej mamy do czynienia z rozkładem wyników, należy stosować narzędzia statystyczne (analiza wariancji, analiza spektralna i testy istotności) do oceny otrzymanych wyników. Z reguły analiza wystarcza do wyboru najlepszej polityki spośród zbadanych. Czasem wyniki wskazują, że potrzebne są dalsze badania (ze zmianą modelu włącznie).
2. Metoda symulacji - przykład
Firma A konkuruje z firmą B na lokalnym rynku w sprzedaży odkurzaczy Rainbow. Badania wykazały, że chłonność rynku wynosi 1040 szt. rocznie. Sugerowana cena detaliczna wynosi 5000 zł, a cena zakupu od producenta - 4000 zł (dla obu firm).
Dyrektor firmy A chce znać cenę, która pozwoli na maksymalizację rocznego zysku. Nie jest to proste, gdyż udział A w rynku zależy od stosunku cen A i B. Firma B zmienia ceny bez uprzedzenia z tygodnia na tydzień.
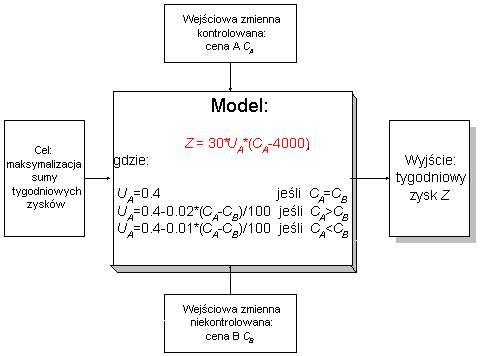
Jeśli obie firmy mają jednakowe ceny, A ma 40% udział w rynku. Jeżeli B ma niższą cenę, A traci z tego poziomu 4% udziału za każde 100 zł różnicy, gdy sytuacja jest odwrotna, A zyskuje 1% udziału za każde 100 zł różnicy.
Przeprowadzenie eksperymentu w sytuacji rzeczywistej byłoby zbyt długotrwałe, a ponadto ryzykowne. Lepiej zastosować metodę prób i błędów nie w stosunku do rzeczywistej sytuacji, lecz jej modelu.
Funkcja celu: maksymalizacja sumy tygodniowych zysków firmy A.
Zmienna kontrolowana (decyzyjna): cena sprzedaży A.
Zmienna niekontrolowana: cena sprzedaży B.
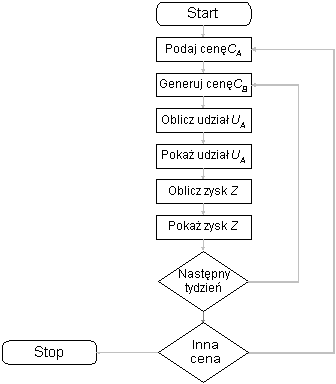
Prowadzimy symulację przez np. 20 tygodni dla cen firmy A zmieniających się co 100 zł (4100, 4200, ..., 4900). Razem daje to 9 przebiegów symulacyjnych.
W każdym przebiegu:
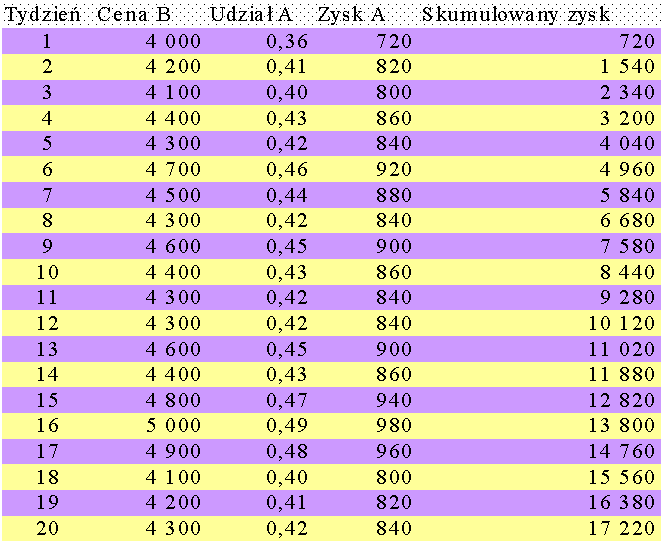

Zgodnie z wynikami zaprezentowanymi w tabeli, spośród zbadanych cen, 4700 zł/sztukę prowadzi do największego skumulowanego zysku.
W praktyce decydent powinien przeprowadzić dłuższe eksperymenty (52 tygodnie), a ceny konkurenta powinny być bardziej uściślone.
Metoda Monte Carlo wywodzi się z poszukiwań prowadzonych podczas II wojny światowej. Naukowcy z laboratorium w Los Alamos chcieli opisać, jak daleko neutrony przenikają przez różne materiały. Zagadnienie było niezmiernie ważne przy projektowaniu urządzeń nuklearnych, a nie istniały odpowiednie metody analityczne. Metoda prób i błędów byłaby zbyt czasochłonna i ryzykowna.
Naukowcy sięgnęli po technikę znaną już od wieku, która została zaniechana ze względu na swą dziwność. Technika ta zakładała użycie znanych fizycznych właściwości i zaobserwowanych prawdopodobieństw do określenia wyniku eksperymentu, który nie mógł być wykonany; oszacowanie wyniku było oparte na przeprowadzonej symulacji eksperymentu. Technice tej nadano nazwę Monte Carlo, gdyż opierała się na tych samych zasadach, co gra hazardowa.
Metoda Monte Carlo to każda metoda wymagająca użycia zachowania losowego do rozwiązania problemu. Metody te są stosowane do szerokich klas problemów deterministycznych i probabilistycznych. Problemy deterministyczne to np. rozwiązywanie równań różniczkowych, znajdowanie pól i objętości, odwracanie macierzy czy obliczanie wartości p. Zastosowania probabilistyczne dotyczą symulacji procesów, które istotnie zawierają zmienne losowe, np. symulacja połączeń telefonicznych przez centralę czy obsługa samochodów na stacji benzynowej.
Zastosowanie metody Monte Carlo do problemów deterministycznych opiera się na prawie wielkich liczb Bernoulliego:
częstość występowania zdarzenia w
n próbach jest zbieżna do prawdopodobieństwa tego zdarzenia, gdy n dąży do nieskończoności.Wychodząc z tego twierdzenia, metoda Monte Carlo może być zastosowana np. do całkowania dowolnych funkcji.
Całkowanie numeryczne oparte na definicji Riemanna jest bardzo dobrą techniką aproksymacji całki z żądaną dokładnością. Zawodzi jednak w przypadku całek nad skomplikowanymi obszarami przestrzeni wielowymiarowych. W tej sytuacji zasadne może być użycie metody Monte Carlo.
Załóżmy, że mamy daną część
R płaszczyzny poprzez określenie jej brzegów jako relacji między dwoma zmiennymi. Chcemy obliczyć pole powie-rzchni R. Wychodzimy od części płaszczyzny Q, która zawiera R, a której pole jest łatwo obliczyć (Q jest zwykle kwadratem). Używając generatora liczb losowych losujemy punkty p1,p2,...pn z obszaru Q. Dla każdego punktu pi sprawdzamy, czy leży on w obszarze R, jednocześnie je zliczając. Liczbę tych punktów oznaczmy P(n).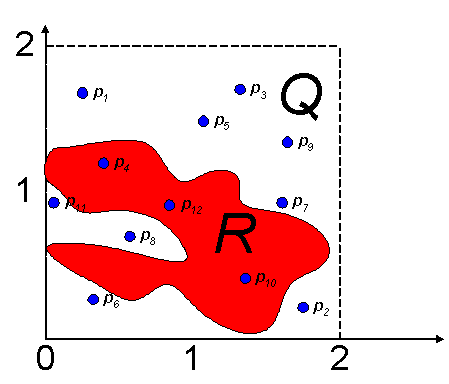
W opisanej sytuacji firma A zna potencjalną rozpiętość cen konkurenta, ale nie ma pewności co do dokładnej jej wartości. Jako że niekontrolowana zmienna wejściowa jest niepewna, model konkurencji cenowej firm A i B jest
de facto modelem stochastycznym. Szczególnie w tej sytuacji symulacja może być wartościowym narzędziem podejmowania decyzji. W tym wypadku konieczne jest generowanie zmiennej wejściowej zgodnie z rzeczywistym rozkładem prawdopodobieństwa.Na podstawie danych historycznych zarząd A oszacował rozkład cen firmy B:

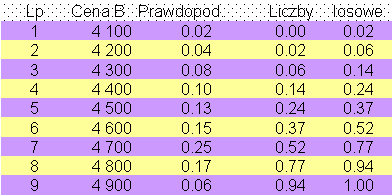
W modelu musimy tak generować ceny B, by były one zgodne z zaobserwowanym rozkładem. Dobrym rozwiązaniem jest wykorzystanie generatora liczb pseudolosowych z przedziału [0...1] w taki sposób, by prawdopodobieństwo wylosowanych liczb było dokładnie takie samo jak prawdopodobieństwo powiązanych cen firmy B.
Liczby losowe związane z cenami firmy B:
Prowadzimy symulację przez np. 20 tygodni dla cen firmy A zmieniających się co 100 zł (4100, 4200, ..., 4900). Razem daje to 9 przebiegów symulacyjnych.
W każdym przebiegu:
Symulowane ceny firmy B:
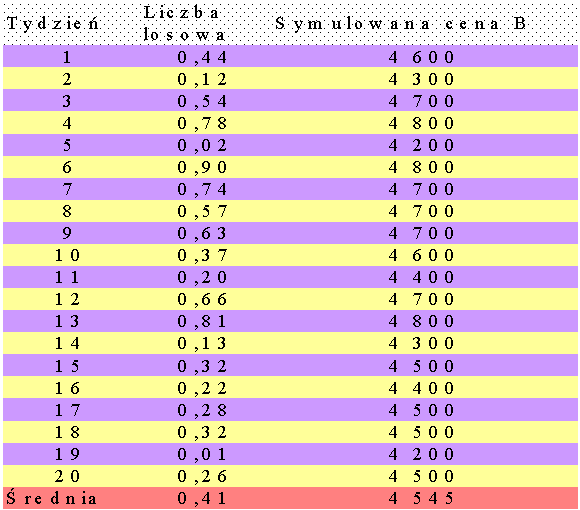
Wyniki dla ceny = 4100
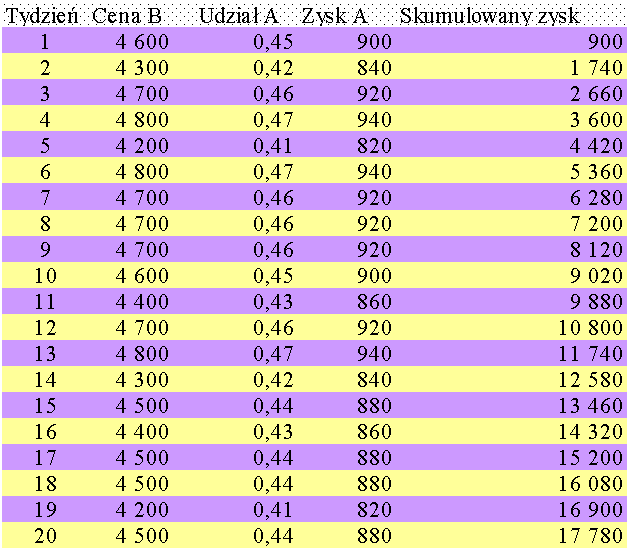
Wyniki dla wszystkich cen

Zgodnie z wynikami zaprezentowanymi w tabeli, spośród zbadanych cen, 4800 zł/sztukę prowadzi do największego skumulowanego zysku.
W praktyce decydent powinien przeprowadzić kilkadziesiąt dłuższych eksperymentów (52 tygod-nie) i zanalizować wariancję zysku.
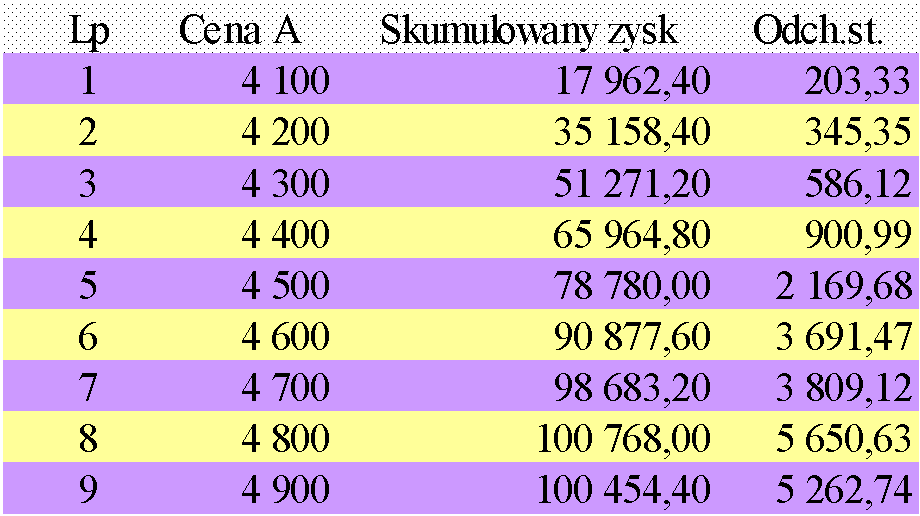
Analiza wyników obejmuje przede wszystkim analizę wariancji dla wielu średnich. Testy te pozwalają na sprawdzenie, czy pewne czynniki regulowane w trakcie eksperymentu (tu: cena A) wywierają wpływ, a jeśli tak, to jaki, na kształtowanie się średnich wartości badanych cech (tu: zysk). W naszym przypadku powinniśmy przeprowadzić tzw. klasyfikację pojedynczą mierzącą wpływ pojedynczego czynnika.
We wszystkich testach analizy wariancji warunkiem koniecznym jest założenie jednorodności wariancji (np. test Bartletta).
Test Bartletta o równości wariancji we wszystkich po
pulacjach normalnych:H0: s12=s22=...=sk2 i H1: nie wszystkie są równe
Z wyników k prób o licznościach ni obliczamy kolejno wariancje w grupach, wariancję ogólną, wartość współczynnika c i wartość statystyki c2. Statystyka ta ma rozkład c2 z k-1 stopniami swobody. Jeśli z porównania c2 z wartością krytyczną c2a otrzymamy c2 >= c2a sprawdzaną hipotezę H0 odrzucamy.
W naszym przypadku:
k = 9, ni = 25 (dla wszystkich i=1,..,k), n = 225,
s2 = 10420641,2, c = 1,015432
c2 = 332,37.
Dla przyjętego poziomu istotności
a = 0,05 i dla 8 (=k-1) stopni swobody wartość krytyczna c2a wynosi 15,507. Ponieważ otrzymaliśmyc2 =332,37>=15,507= c2a
sprawdzaną hipotezę H
0 odrzucamy. Oznacza to, iż udowodniono różny stopień rozproszenia zysku przy badanych 9 poziomach cen wyrobu.W celu określenia czy wyniki istotnie różnią się od siebie, należy sprawdzić hipotezę, że średnie wartości uzyskanych rozwiązań są jednakowe, wobec hipotezy alternatywnej, że średnia wartość zysku
Zi otrzymana przy cenie Ci jest mniejsza (większa) niż średnia Zj otrzymana przy cenie Cj:H0: Zi = Zj i H1: Zi < Zj.
Jeśli nie są znane odchylenia standardowe obserwowanej zmiennej w obu zbiorowościach i próby są duże, to sprawdzianem hipotezy H
0 może być wyrażenie: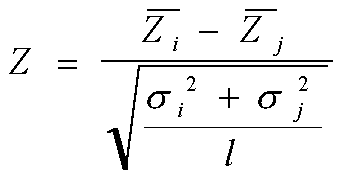
Statystyka Z ma rozkład normalny N(0,1). Hipotezę H0 sprawdzano przy poziomie istotności a=0,01, dla którego za=-2,33 (przy lewostronnym obszarze krytycznym).
Wyniki testów statystycznych
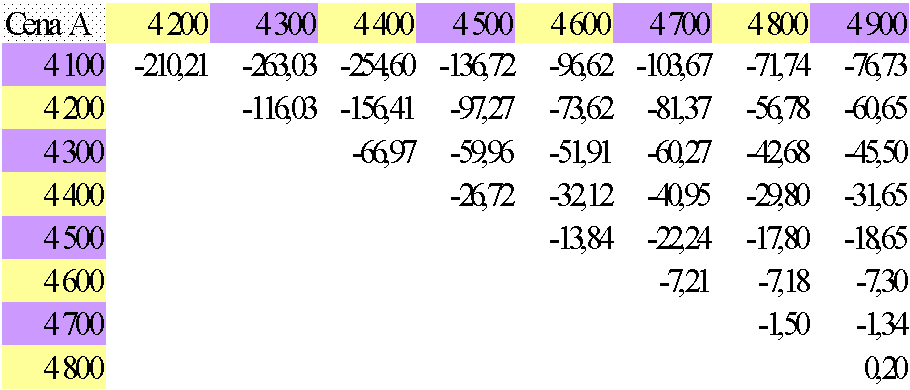
4. Statystyczne aspekty symulacji
We wszystkich symulacjach probabilistycznych występują elementy losowe (rozkład cen, czasy obsługi itp.). Dlatego wynik symulacji nie jest dokładną odpowiedzią, lecz szeregiem liczb o losowym rozkładzie.
W symulacjach występuje wiele problemów statystycznych, specyficznych i nie - dla tej metody:
W przypadku symulacji stochastycznej podstawowe znaczenie ma generowanie liczb z rozkładu jednostajnego, gdyż przez jego przekształcenie można uzyskać liczby losowe o dowolnym rozkładzie.
Rozkład jednostajny to taki rozkład, w którym prawdopodobieństwa wylosowania dowolnej wartości z danego przedziału (np. [0...1]) są sobie równe.
Losowy oznacza, że nie da się przewidzieć, jakie liczby otrzymamy.
Należy generować ciąg takich liczb, które:
Spośród różnych metod otrzymywania liczb losowych (specjalne urządzenia, rzuty kostkami, tablice) najwygodniejsze i najszybsze jest generowanie liczb za pomocą zależności rekurencyjnej. Generowane w ten sposób liczby nie są, ściśle rzecz ujmując, losowe i
dlatego nazywamy je liczbami pseudolosowymi. Liczby te spełniają warunki 1, 5 i 6, natomiast stopień spełnienia pozostałych warunków zależy od własności stosowanych zależności rekurencyjnych.Metody generowania liczb pseudolosowych opierają się na koncepcji
kongruencji. Dwie liczby całkowite a i b są w konkruencji z modułem m, jeśli ich różnica jest liczbą całkowitą, stanowiącą wielokrotność m. Relację kongruencji zapisujemy jako: a º b (mod m), a jest kongruentne z b modulo m.Przykład: 1897 º
7 (mod 5)Dla wszystkich metod opartych na kongruencji liczb podstawowe znaczenie ma następujący wzór rekurencyjny:
ni+1 º [a*ni + b] (mod m)
gdzie
ni, a, b, m są liczbami całkowitymi nieujemnymi, a - stały mnożnik, b - stała dodatkowa, n0 - wartość początkowa.
Następującymi kolejno po sobie liczbami {ni} są całkowicie zdeterminowane liczby całkowite tworzące ciąg reszt dla mod m. Oznacza to, że wszystkie ni < m.
Z liczb występujących w ciągu {
ni} można otrzymać właściwe liczby z przedziału [0...1] tworząc ciąg {ri} = {ni/m}.Czy istnieje najmniejsza wartość
i = h, że nh= n0, gdzie h jest okresem ciągu? Jeśli bowiem i = h, to nh+1 = n1, nh+2 = n2, itd. Można wykazać, że taka liczba h zawsze istnieje i że jej wartość maksymalna zależy od m.Najpopularniejszą metodą tworzenia liczb pseudolosowych opartą na kongruencji jest generator multiplikatywny, w którym stała dodatkowa
b=0:ni+1 º a*ni (mod m)
Generator ten ma b.dobre własności statystyczne tzn. liczby nie są ze sobą skorelowane i mają rozkład równomierny, a przy założeniu pewnych warunków na
a, n0 i m. możemy zapewnić maksymalny okres ciągów h. Ponadto ciągi te można powtarzać, a same obliczenia są b.szybkie.Podano wiele reguł doboru a, n0 i m. Dla komputerów dwójkowych o słowie 32-bitowym przyjmuje-my, że m=231-1 (=2147483647). Algorytm wygląda następująco:
Własności statystyczne liczb pseudolosowych powinny odpowiadać własnościom liczb losowych (niezależne, równe szanse). Jako że liczby generowane przez programy komputerowe nie są liczbami losowymi w powyższym sensie, muszą być pod-dawane testom statystycznym, które pozwalają uznać te liczby za “prawdziwie” losowe lub nie.
Z drugiej strony jak zauważył Marshall “wydaje się, że fałszywy charakter losowości wygenerowanej sekwencji nie wpływa na obliczenia Monte Carlo, w każdym razie nie wykryły tego różne testy statystyczne, którym te sekwencje były poddane i przez które przeszły z zupełnym powodzeniem”.
Testy statystyczne, które umożliwiają testowanie losowości liczb pseudolosowych:
Test wskaźnika struktury
Niech p oznacza frakcję takich elementów w zbiorowości statystycznej, które mają pewną wyróżnioną cechę (0<=p<=1); parametr może być interpretowany jako prawdopodobieństwo wylosowania z tej zbiorowości elementu z wyróżnioną cechą.
H0: p = p0 wobec H1: p <> p0
Niech X oznacza liczbę elementów z cechą wyróżnioną w próbie losowej, a n - liczność próby. Zmienna losowa Z
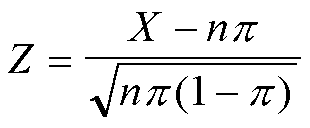
ma rozkład normalny
N(0,1).Wykonując operacje matematyczne na liczbach losowych o rozkładzie równomiernym [0, 1], można tworzyć liczby losowe o innych rozkładach.
Ciąg liczb
R’=1-R (R={ri}) ma też rozkład jednostajny w przedziale [0, 1] i nazywany jest ciągiem przeciwnym. Ciągi takie są ważnym środkiem zmniejszania wariancji w symulacjach stochastycznych.Rozkład prostokątny w przedzi
ale [a, b]P = a+(b-a)*R ma rozkład prostokątny w [a, b].

Zmienne losowe o danym rozkładzie dyskretnym
Wykonujemy mapowanie liczb losowych z [0, 1] na dystrybuantę:
Zmienne losowe o danym rozkładzie ciągłym
Ogólna metoda polega na odwróceniu dystrybuanty F(x).
Weź liczbę losową
R o rozkładzie jednostajnym w przedziale [0, 1] i rozwiąż równanie F(X) = R lub F(X) = 1-R . Wtedy X ma szukany rozkład i nazywa się liczbą losową o dystrybuancie F(x).Liczby losowe o rozkładzie wykładniczym
F(x) = 1-e-lx (x>=0, wartość oczekiwana 1/l).
Weź liczbę losową
R o rozkładzie jednostajnym w przedziale [0, 1] i oblicz X = -ln(R)/l.Dowód
F(X) = 1-R
1-e-lX = 1-R
e-lX = R
-lX = ln(R)
X = -ln(R)/l
Ważnym zastosowaniem liczb losowych o rozkładzie wykładniczym jest generowanie tzw. procesów Poissona.
Liczby losowe o rozkładzie normalnym
Przy użyciu dwóch niezależnych liczb losowych
R1 i R2 o rozkładzie jednostajnym w [0, 1] można otrzymać dwie niezależne liczby losowe o rozkładzie normalnym N(0,1). Jest to tzw. przekształcenie Boxa-Mullera:N1 = (-2 ln(R1))1/2 cos(2piR2)
N2 = (-2 ln(R1))1/2 sin(2piR2)
Tworząc liczby
m+s N1 i m+s N2 otrzymujemy zmienne losowe o rozkładzie N(m,s).Analiza wariancji opiera się na rozkładzie estyma-torów wariancji wokół prawdziwych wariancji z populacji normalnych. Istotą a.w. jest rozbicie na addytywne składniki sumy kwadratów wariancji całego zbioru wyników. Porównanie wariancji wynikającej z działania danego czynnika oraz waiancji resztowej (mierzącej losowy błąd) daje odpowiedź, czy dany czynnik odgrywa istotną rolę w kształtowaniu się wyników eksperymentu.
Klasyfikacja pojedyncza
Sumę kwadratów wariancji ogólnej rozbija się na dwa składniki mierzące zmienność między grupami i wewnątrz grup (resztową). Porównując te wariancje testem
F rozstrzygamy, czy średnie grupowe różnią się istotnie od siebie czy nie. Jeśli podział na grupy przebiegał ze względu na różne poziomy badanego czynnika, to można wykryć w ten sposób wpływ poziomu na wartość badanej cechy.Danych jest k populacji normalnych N(mi,si), i=1,...,k. Wariancje wszystkich populacji są równe (nie muszą być znane). Z każdej z tych populacji wylosowano niezależnie próby o liczebności ni. Wyniki prób oznaczone są xij (j=1,...,ni), przy czym xij=mi+eij, gdzie eij jest wartością zmiennej losowej nazywanej składnikiem losowym o rozkładzie N(0,s).
H0: m1=m2=...=mk wobec H1: nie wszystkie średnie są równe
Jeśli F>=Fa, to hipotezę o równości średnich w badanych populacjach należy odrzucić, co oznacza udowodnienie istotnego wpływu poziomu czynnika na te populacje.
Jeśli odrzucono hipotezę H0 należy w dalszym etapie analizy wyników zastosować metodę porównywania wielokrotnego (badanie istotności różnic między wartościami średnimi dla wszystkich par czynnika).
Jeśli chcemy zbadać wpływ poziomu dwóch czynników stosujemy klasyfikację podwójną.
Znane są różne metody zmniejszania nakładu pracy (liczby eksperymentów) niezbędnego do osiągnięcia danego poziomu ufności wyników. Jeśli wykona się
n niezależnych obserwacji pewnej wielkości, których odch. stand. jest równe s, to błąd standardowy średniej tych obserwacji wyniesie s/n1/2. Jeśli wykonamy dwa warianty eksperymentu powtarzając je n1 i n2 razy, ich wyniki mają odch. stand. s1 i s2, to jednakową dokładność otrzymamy gdys1/n11/2=s2/n21/2 czyli n1/n2=s12/s22.
Ogólnie: jeśli pewien rodzaj eksperymentu redukuje wariancję k-krotnie, to liczbę powtórzeń można zmniejszyć również k-krotnie.
Powtarzanie ciągów liczb losowych
Celem symulacji jest zazwyczaj porównanie różnych możliwości. W takim przypadku eksperymentator powinien odtwarzać i ponownie używać tego samego ciągu zdarzeń do różnych przebiegów (ciąg taki jest funkcją liczb pseudolosowych). W ten sposób uzyskuje pożądane wyniki za pomocą znacznie mniejszej próbki, niż gdyby generował niezależne ciągi w każdym przebiegu.
Ciągi przeciwne liczb losowych R’=1-R
W tym przypadku eksperymentator wykonuje przebiegi parami korzystając z ciągu liczb losowych i ciągu doń przeciwnego. Następnie należy obliczyć średnie par jako wyniki eksperymentu. Metoda ta zwykle kilkukrotnie zmniejsza koszt obliczeń w porównaniu do użycia ciągów zupełnie niezależnych liczb losowych.
Motywacje dla symulacji kolejek wynikają ze złożoności systemu:
Bez tych ograniczeń model można rozwiązać analitycznie.
Przypuśćmy, że czas przybycia i czas obsługi dane są następującymi rozkładami empirycznymi:
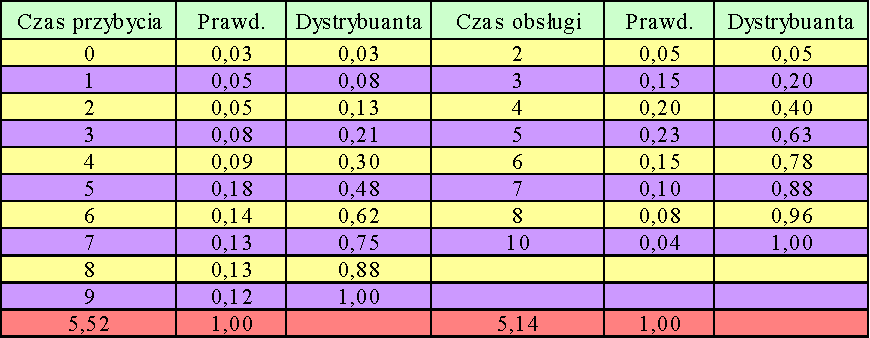
Przebieg symulacji:
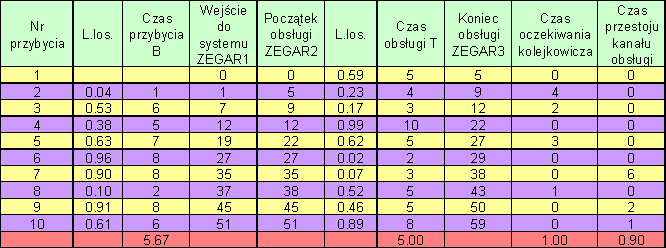
Ten rodzaj symulacji nazywa się
od zdarzenia do zdarzenia, gdyż kolejne kroki symulacji związane są z pojawianiem się kolejnych zdarzeń. W tym przypadku zdarzeniami są przybycie jednostki, rozpoczęcie i zakończenie obsługi, a zegar symulacji przesuwa się o czas potrzebny na zajście następnego zdarzenia.Alternatywnym sposobem reprezentacji upływu czasu jest dzielenie badanego okresu na ściśle określone niezmienne przedziały i obserwowanie zachowań modelu w kolejnych chwilach czasu. To podejś
cie do symulacji nazywane jest symulacją ze stałym krokiem.Systemy zapasów są symulowane, jeśli analityczne rozwiązanie nie jest możliwe:
Jednym z najszerzej stosowanych modeli zapasów jest RPM (Reorder Point Model); należy tak dobrać punkt ponawiania zamówień i ilość zamawianą, by zminimalizować sumę średnich kosztów utrzymywania, zamawiania i braku zapasów w jednostce czasu.
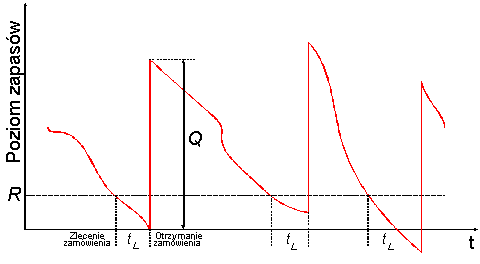
Stochastyczny model systemu zapasów- przykład
Artysta s.c. zaopatruje grafików w ponad 500
produktów. Firma używa modelu analitycznego dla określania ilości i
punktów zamówienia. Model ten nie sprawdza się dla jednego
produktu: zapotrzebowanie nań jest stosunkowo niskie a przy tym zmienne, ponadto
czasy dostaw nie są stałe. Powoduje to niejednokrotny brak towaru w magazynie, a
co za tym idzie - potencjalną stratę sprzedaży i niezadowolenie
klientów.
Na podstawie danych historycznych ustalono następujące
rozkłady:
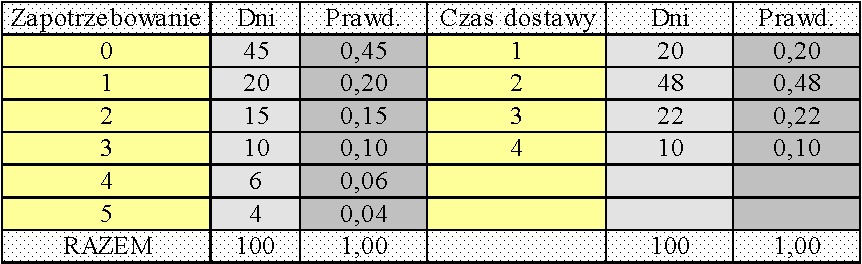
Znane są lub oszacowane:
Ku - jednostkowy koszt utrzymania zapasu
Kz - koszt realizacji zamówienia,
Kb - jednostkowy koszt braku pozycji w
magazynie.
Zarządzający pragną zminimalizować łączne koszty
KR związane z zapasami. Zaproponowano dwie polityki:Q = 20 sztuk, R = 2 sztuki,
Q = 10 sztuk, R = 5 sztuk.
Cel: minimalizacja średniego kosztu KR:
KR = Kz + Wm*Ku + Bp*Kb
Zmienne decyzyjne: Q i R.
Zmienne wejściowe niezależne:
P (zapotrzebowanie) i CD (czas dostawy).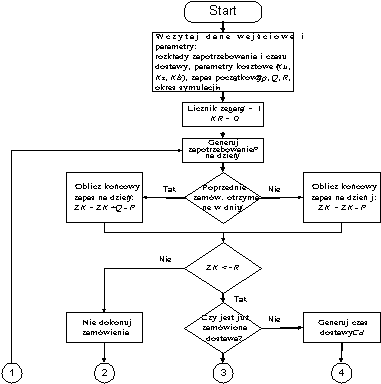
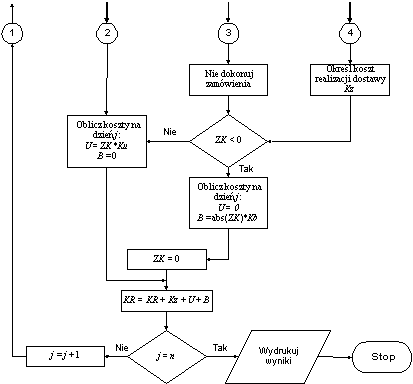
Wyniki dla Q=20 i R=2 oraz Kz=70 zł, Ku=0,4 zł/szt, Kb=150 zł/szt.
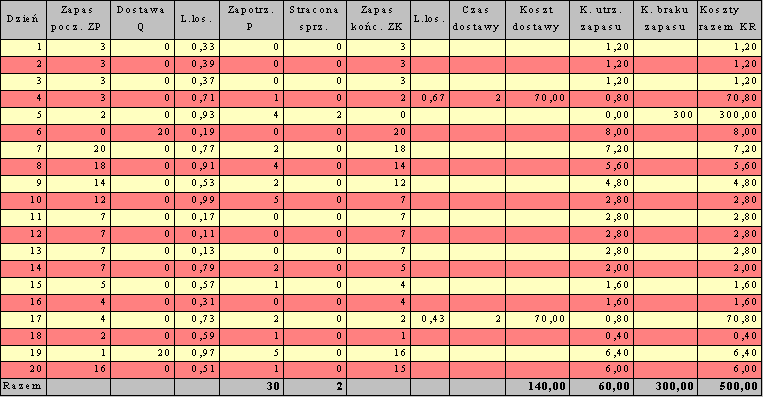
Wyniki dla Q=10 i R=5 oraz Kz=70 zł, Ku=0,4 zł/szt, Kb=150 zł/szt.
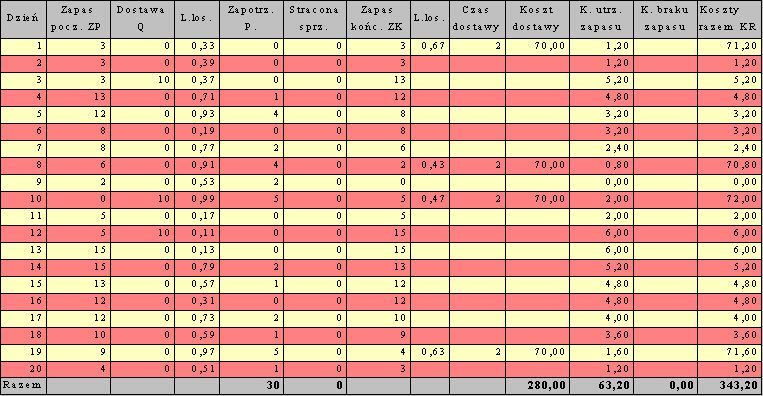
Punkt startowy można wybrać losowo, ale lepiej wyjść od rozwiązania osiągniętego analitycznie:
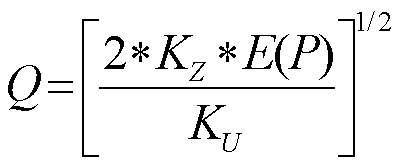
![]()