Wprowadzenie do problemu szeregowania zadań na pojedynczej maszynie

---

Właściwa ilość wyrobów powinna być wyprodukowana i dostarczona w ściśle określonym czasie. Planowane zadania powinny być wykonane punktualnie, gdyż zarówno zbyt wczesne jak i zbyt późne dostarczenie wyrobów jest niepożądane. Zbyt wcześnie zakończone zadania powodują wzrost kosztów utrzymania zapasów produkcji gotowej u producenta, a tym samym niepotrzebne zamrożenie środków obrotowych. Z kolei zakończenie wykonywania zadań po ustalonym terminie powoduje niezadowolenie klientów i, w dłuższej perspektywie, może skończyć się ich odejściem do innych wytwórców.
Problemy tego typu są opisywane i studiowane w dziedzinie nauk zarządzania począwszy od lat siedemdziesiątych XX wieku. W 1977 roku Sidney opisał jednomaszynowy problem minimalizacji odchyleń czasów wykonania od pożądanych terminów i podał algorytm jego rozwiązania. Ta pionierska praca była w następnych latach rozszerzana w wielu różnych kierunkach. Wbrew pozorom problem ten jest realistyczny: w wielu praktycznych przypadkach istnieją tzw. wąskie gardła i właśnie na tę pojedynczą maszynę powinno być zorientowane planowanie.
Harmonogramowanie produkcji polega na podziale zleceń klientów na partie produkcyjne (zadania) oraz określeniu terminów rozpoczęcia i zakończenia partii produkcyjnych na poszczególnych maszynach. Wynikiem tego jest ustalenie kolejności wykonania partii produkcyjnych na wszystkich maszynach. W przypadku układania harmonogramu dla jednej maszyny możemy przyjąć, że liczba zadań n jest skończona i znana wcześniej, przy czym wszystkie zadania są gotowe do wykonania jednocześnie (tzn. proces obsługi może się zacząć od dowolnego zadania i). Czas wykonania zadania p_i jest wcześniej znany i nie zależy od uporządkowania (każde zadanie może być wykonane bez przezbrajania maszyny bądź czas przezbrajania nie zależy od poprzedniego zadania i jest wliczony do czasu wykonywania zadania). Ponadto każde zadanie ma podany termin dyrektywny (planowy) d_i, a przerywanie wykonywania zadań nie jest dopuszczalne. Zadanie jest opóźnione, jeśli jego moment zakończenia C_i przekracza termin dyrektywny. Zadanie jest wyprzedzone, jeśli jego moment zakończenia jest wcześniejszy niż termin planowany. Wyprzedzenie i opóźnienie zadania są obliczane jako E_i=max{d_i - C_i;0} oraz T_i=max{C_i - d_i;0}. Powyższe zależności ilustruje rysunek.

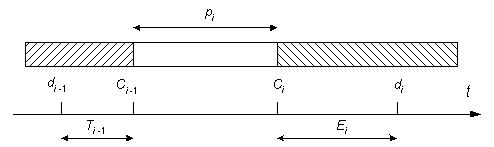
Celem jest znalezienie dopuszczalnej sekwencji zadań S, która minimalizuje zadaną funkcję celu, np. ważoną sumę wyprzedzeń i opóźnień:

gdzie a - współczynnik wagowy wyprzedzenia (np. koszt magazynowania wyrobów gotowych w jednostce czasu), b - współczynnik wagowy opóźnienia (np. koszt straconej produkcji).